Bayesian Inference Models for Insightful Data Analysis
Welcome to the fascinating world of Bayesian Inference Models – where data analysis meets insightful decision-making! Have you ever wondered how to unlock hidden patterns within your data or make predictions with confidence? Look no further, as we delve into the intricacies of Bayesian models and explore their real-world applications. Get ready to decode complexity and harness the power of Bayesian Inference for a deeper understanding of your data like never before! Let’s embark on this exciting journey together.
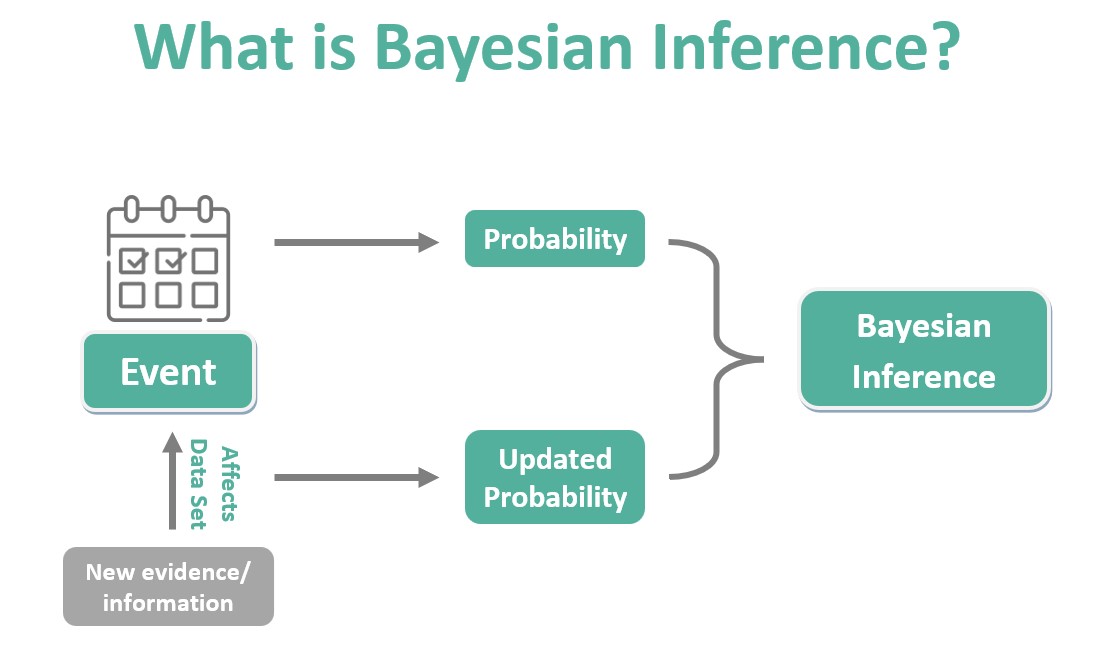
Understanding Bayesian Inference: What is it and why is it important?
Bayesian Inference is a statistical method used to update beliefs about the likelihood of an event based on new evidence. It allows for the incorporation of prior knowledge, making it a powerful tool in data analysis. Unlike frequents approaches, Bayesian models provide a framework for quantifying uncertainty and making probabilistic statements.
One key aspect of Bayesian Inference is its ability to handle complex problems with multiple sources of information. By combining prior beliefs with observed data, Bayesian models offer a flexible and robust way to analyze diverse datasets. This adaptive nature makes them particularly valuable in situations where traditional methods may fall short.
Furthermore, Bayesian models can help researchers make more informed decisions by providing estimates along with measures of uncertainty. This nuanced approach allows for better risk assessment and decision-making under uncertainty. Understanding Bayesian Inference opens up new possibilities for extracting meaningful insights from data and driving informed strategies forward.
The Benefits of Using Bayesian Inference Models in Data Analysis
Bayesian Inference models offer a unique approach to data analysis, providing a flexible framework that allows for the incorporation of prior knowledge and updating beliefs based on new evidence. By leveraging probability distributions, these models can handle uncertainty with ease, making them particularly useful in complex decision-making scenarios.
One of the key benefits of Bayesian Inference is its ability to quantify uncertainty in a principled manner, offering more informative results compared to traditional statistical methods. This means that not only do you get insights from the data itself, but also an understanding of how confident you can be in those insights.
Furthermore, Bayesian models allow for the seamless integration of different sources of information, enabling analysts to make more robust conclusions by combining data from various sources. This integrative approach often leads to richer and more accurate predictions.
Incorporating Bayesian Inference models into your data analysis toolkit can lead to more nuanced and insightful interpretations that go beyond simple point estimates or p-values.
Real-World Applications of Bayesian Inference
Bayesian Inference models have found a wide range of applications across various industries, showcasing their versatility and effectiveness in making informed decisions. In the field of healthcare, Bayesian methods are used to predict patient outcomes based on medical data, aiding doctors in personalized treatment plans.
Furthermore, in finance, Bayesian models help analyze market trends and risks for better investment strategies. This enables financial institutions to optimize their portfolios and minimize losses. In marketing, businesses utilize Bayesian networks to understand customer behavior patterns and tailor marketing campaigns that resonate with target audiences.
Moreover, in environmental studies, Bayesian analysis is employed to forecast climate changes and assess the impact of human activities on ecosystems. These real-world applications highlight the power of Bayesian Inference models in driving impactful decision-making processes across diverse sectors.
Step-by-Step Guide to Implementing Bayesian Inference Models
To start implementing Bayesian Inference models, you first need to define your research question or problem. This step is crucial as it sets the foundation for your entire analysis. Next, gather relevant data that will help you answer your research question. Remember, the quality of your data directly impacts the accuracy of your results.
Once you have your data in hand, choose a suitable prior distribution that represents what you know about the parameters before seeing the data. Select an appropriate likelihood function based on the relationship between the parameters and observed data.
After setting up your prior and likelihood functions, apply Bayes’ theorem to update your beliefs about the parameters given the observed data. Use computational methods like Markov Chain Monte Carlo (MCMC) to estimate posterior distributions. Evaluate model fit and make any necessary adjustments before drawing conclusions from your analysis.
Continuously refine and iterate through this process to improve model performance and gain deeper insights into your data. By following these steps diligently, you can unleash the power of Bayesian Inference models in unlocking valuable information from complex datasets.
Challenges and Limitations of Bayesian Inference
When it comes to Bayesian Inference, there are certain challenges and limitations that data analysts may encounter. One common challenge is the complexity of model implementation. Bayesian models can sometimes be computationally intensive, requiring advanced statistical knowledge for proper execution.
Another limitation is the need for prior beliefs or assumptions in Bayesian analysis. Selecting appropriate priors can be subjective and may influence the final results, leading to potential biases in the analysis.
Additionally, interpreting and communicating results from Bayesian models can pose a challenge. The probabilistic nature of Bayesian inference may require more nuanced explanations compared to traditional frequents approaches.
Furthermore, validating complex Bayesian models with real-world data can be tricky due to over fitting or under fitting issues. Ensuring the model’s predictive power while avoiding these pitfalls requires careful consideration and expertise.
Despite these challenges and limitations, mastering Bayesian Inference can unlock valuable insights from complex datasets and enhance decision-making processes in various fields of study.
How to Choose the Right Model for Your Data
When it comes to choosing the right model for your data analysis, there are a few key factors to consider. Assess the nature of your data – is it continuous or categorical? This will help determine which Bayesian inference model would be most suitable.
Think about the complexity of your analysis. If you have a large dataset with many variables, a more sophisticated Bayesian model might be needed to capture all relevant patterns and relationships.
Additionally, consider the assumptions of different models. Some may assume linearity while others allow for non-linear relationships. Choose a model that aligns with the underlying structure of your data.
Don’t forget about interpretability. A simpler model may be preferred if you need to easily explain and communicate results to stakeholders.
By carefully evaluating these factors, you can select the Bayesian inference model that best fits your unique dataset and research questions without compromising accuracy or efficiency in your analysis.
Conclusion
Bayesian Inference Models offer a powerful and flexible approach to data analysis. By incorporating prior knowledge and updating beliefs based on new evidence, these models provide a nuanced understanding of complex systems. From predicting customer behavior in marketing to diagnosing medical conditions, Bayesian Inference has diverse real-world applications. While there are challenges and limitations to consider when implementing these models, the benefits far outweigh the drawbacks for those seeking insightful and accurate data analysis. Choosing the right model for your specific dataset is crucial for achieving meaningful results. Embracing Bayesian methods can unlock a deeper understanding of uncertainty and variability in your data, leading to more informed decision-making processes across various industries. Start decoding complexity with Bayesian Inference Models today and revolutionize the way you analyze data!